When The P-Value is Less Than 0.05: Understanding Statistical Significance
When p value is less than 0.05, it indicates that the probability of observing the obtained results by random chance is less than 5%, providing evidence to reject the null hypothesis in favor of the alternative hypothesis, suggesting a statistically significant effect or relationship between the variables being studied.
What Does “When P Value is Less Than 0.05” Mean?
When p value is less than 0.05, the probability of observing the obtained results, or more extreme ones, under the assumption that the null hypothesis is true, is less than 5%. This threshold is widely used as a benchmark for statistical significance, implying that the observed effect or relationship between the studied variables is unlikely to have occurred by chance alone. In such cases, researchers typically reject the null hypothesis in favor of the alternative hypothesis, suggesting a statistically significant effect or relationship exists. However, it is essential to consider the context, effect size, and potential biases when interpreting results with a p-value less than 0.05.
Highlights
- P-value < 0.05 indicates evidence against the null hypothesis, suggesting a statistically significant effect or relationship.
- Sir Ronald A. Fisher introduced the 0.05 threshold in 1925, striking a practical balance between Type I and Type II errors.
- The 0.05 threshold is arbitrary; researchers may need more stringent or lenient significance levels depending on the context.
- P-values do not provide information about the magnitude or practical importance of the observed effect.
- Confidence intervals help convey the precision of the estimated effect, complementing P values.
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Introduction to P-Values and Statistical Significance
When conducting research, it is essential to understand the role of p-values and statistical significance in determining the validity of your results. P-values are a fundamental concept in statistics and are commonly used to assess the strength of the evidence against a null hypothesis.
The p-value, or probability value, is a measure that helps researchers assess whether the observed data are consistent with the null hypothesis or if there is a significant deviation from it. In other words, the p-value quantifies the probability of observing the obtained results (or more extreme) if the null hypothesis were true. For example, a smaller P value indicates that the observed data is less likely to have occurred by random chance alone, suggesting that there may be an effect or relationship between the variables being studied.
Statistical significance is a term that describes the likelihood that a relationship between two or more variables is caused by something other than random chance. A statistically significant result indicates that the observed effect is unlikely to be due to chance alone, providing evidence against the null hypothesis. The level of statistical significance is often denoted by an alpha level (α), which represents the threshold for determining whether a result is statistically significant. The most commonly used alpha level is 0.05, meaning that there is a 5% chance of falsely rejecting the null hypothesis if it is true.
When p value is less than 0.05, it implies that the probability of observing the obtained results by random chance is less than 5%, providing evidence to reject the null hypothesis in favor of the alternative hypothesis. This threshold has become a widely accepted standard for determining statistical significance in various research fields.
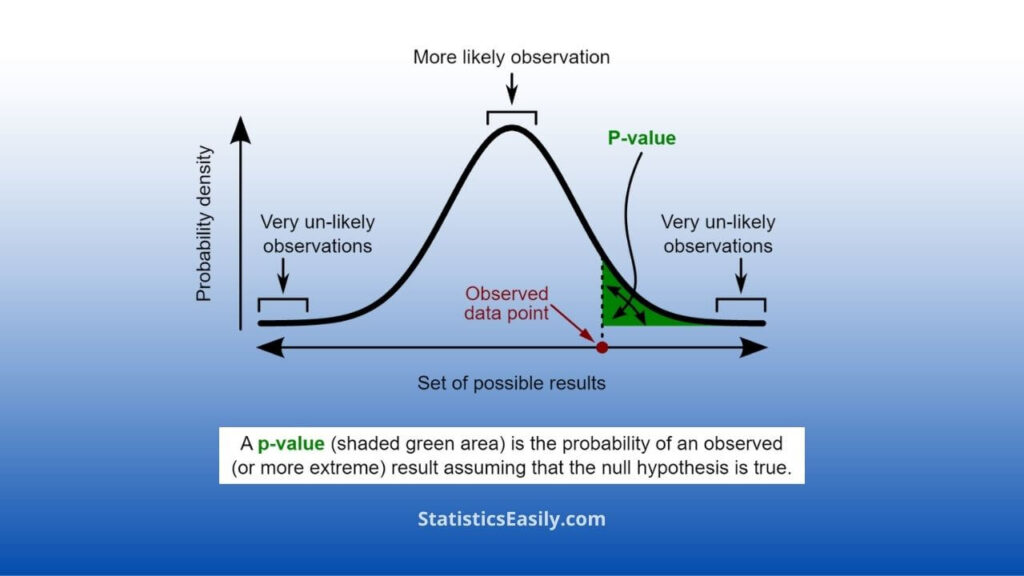
Why a Threshold of 0.05 is Commonly Used?
The threshold of 0.05 for determining statistical significance has been widely adopted across various research fields. But why has this specific value become the standard, and what is its rationale? To understand the origin and significance of the 0.05 threshold, we need to delve into the history of statistical hypothesis testing and the contributions of notable statisticians.
The 0.05 threshold can be traced back to the work of Sir Ronald A. Fisher, a prominent British statistician, and geneticist who played a crucial role in developing modern statistical methods. In his 1925 book, “Statistical Methods for Research Workers,” Fisher introduced the concept of the p-value and proposed the 0.05 level as a convenient cutoff point for determining statistical significance. Fisher’s choice of 0.05 was somewhat arbitrary. Still, it provided a reasonable balance between the risk of false positives (Type I errors) and false negatives (Type II errors). By setting the threshold at 0.05, researchers could manage the risk of falsely rejecting the null hypothesis while maintaining sufficient power to detect true effects.
Over time, the 0.05 threshold gained traction and became a widely accepted convention in statistical hypothesis testing. This widespread adoption can be attributed to several factors, including the desire for a uniform standard to facilitate the comparison of research results and the need for a simple, easily understood criterion for determining statistical significance.
It is important to note that a 0.05 threshold is not inherently superior to other possible thresholds, such as 0.01 or 0.10. The appropriate significance level depends on the specific research context, the consequences of making errors, and the desired balance between the risks of Type I and Type II errors. In addition, more stringent thresholds may be adopted in some fields to reduce the likelihood of false positives. In contrast, in others, a more lenient threshold may be appropriate to minimize the risk of false negatives.
Interpreting Results When P Value is Less Than 0.05
When p value is less than 0.05, it suggests that the observed data provide evidence against the null hypothesis (H0), indicating a statistically significant effect or relationship between the studied variables. However, interpreting these results requires careful consideration of the context, effect size, and potential biases.
Context: Ensure that the research question, study design, and data collection methods are appropriate for the investigated problem. A statistically significant result should be considered in the context of the study’s purpose and existing scientific knowledge.
Effect Size: While a p-value less than 0.05 indicates statistical significance, it does not provide information about the size or practical importance of the observed effect. Researchers should calculate and report effect sizes, such as Cohen’s d or Pearson’s correlation coefficient, to provide a more comprehensive understanding of the results.
Confidence Intervals: Besides the p-value, researchers should report confidence intervals to convey the precision of the estimated effect. A narrow confidence interval suggests the estimate is more precise, while a wider interval implies greater uncertainty.
Multiple Testing: The risk of false positives (Type I errors) increases when performing multiple hypothesis tests. Researchers should apply appropriate corrections, such as the Bonferroni or false discovery rate methods, to control the increased risk.
Reproducibility and Replicability: A statistically significant result should be considered preliminary evidence requiring further investigation. Reproducing the study using the same methods or replicating it with a different sample helps to validate the findings and increase confidence in the results.
Potential Biases: Researchers should consider potential sources of bias, such as selection bias, measurement error, and confounding variables, which may influence the results. Conducting sensitivity analyses and adjusting for potential biases can ensure more robust findings.
Limitations and Misconceptions Around P Values
Despite widespread research, p-values have several limitations and often need to be understood. First, researchers must be aware of these issues to avoid drawing incorrect conclusions from their results. Some common limitations and misconceptions surrounding P values include:
P-values are not a measure of effect size: A p-value indicates the strength of evidence against the null hypothesis but does not provide information about the magnitude or practical importance of the observed effect. Therefore, researchers should report effect sizes alongside p-values to ensure a comprehensive understanding of their results.
P-values do not provide direct evidence for the alternative hypothesis: A p-value less than 0.05 suggests that the H0 (null hypothesis) is unlikely but does not prove that the H1 (alternative hypothesis) is true. Therefore, researchers should be cautious about overstating their conclusions and consider alternative explanations for their findings.
The arbitrary nature of the 0.05 threshold: A 0.05 threshold for determining statistical significance is somewhat arbitrary and may not be appropriate for all research contexts. Depending on the consequences of Type I and Type II errors, researchers may need to adopt more stringent or lenient significance levels.
P-values are sensitive to sample size: As the sample size increases, p-values become smaller, making it easier to detect statistically significant effects even when they are not practically important. Therefore, researchers should consider the impact of sample size on their results and focus on effect sizes and confidence intervals to assess the practical importance of their findings.
Misinterpretation of p-values: P-values are often misinterpreted as the probability that the H0 (null hypothesis) is true or as the probability of making a Type I error. However, a p-value represents the probability of observing the obtained results (or more extreme) if the null hypothesis were true, not the probability of the null hypothesis itself.
Overemphasis on statistical significance: The focus on p-values and statistical significance can lead to an overemphasis on the importance of statistically significant results, potentially neglecting important findings with P values greater than 0.05. Researchers should consider the broader context of their results and prioritize the practical importance of their conclusions rather than solely focusing on statistical significance.
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Recommended Articles
If you found this article insightful, don’t miss out on our other informative and engaging articles on p-values and statistical significance on our blog. Expand your knowledge and stay up-to-date with the latest trends and best practices in data analysis by exploring our expertly crafted content.
- What Does The P-Value Mean?
- What Does The P-Value Mean? Returns
- When is P Value Significant? Understanding its Role in Hypothesis Testing
- Exploring the Scenario when p is 0.051 or higher (p ≥ 0.051)
- P-values and significance (External Link)
- A Guide to Hypotheses Tests (Story)
- When is P Value Significant? (Story)
- Understanding P-Values (Story)
Frequently Asked Questions (FAQs)
It indicates that there’s less than a 5% chance of observing the obtained results by random chance alone, suggesting statistical significance.
Sir Ronald A. Fisher proposed the 0.05 threshold as a practical balance between Type I and Type II errors, and it became widely adopted.
P-value measures evidence against the null hypothesis, while effect size quantifies the magnitude or practical importance of the observed effect.
Confidence intervals convey the precision of the estimated effect, providing additional context to the p-value.
Apply corrections like the Bonferroni or false discovery rate methods to control the increased risk of false positives.
Reproducing and replicating studies helps validate findings, increase confidence in results, and minimize the risk of false positives.
Biases like selection bias, measurement error, and confounding variables can influence results, leading to incorrect conclusions.
Larger sample sizes tend to produce smaller P values, making it easier to detect statistically significant effects, even if they’re not practically important.
Overemphasis on statistical significance can lead to neglecting important findings with p-values > 0.05, skewing research focus and conclusions.
Interpret results by considering research context, effect size, confidence intervals, multiple testing, reproducibility, and potential biases. Exercise caution and corroborate findings with additional research.








