Chi Square Calculator: Enhance Your Data Analysis Skills

You will learn how the Chi Square Calculator can become an indispensable tool in your statistical analysis arsenal.

Introduction

In the world of data science and statistical analysis, the Chi-Square Test stands out as a fundamental tool for evaluating the independence of categorical variables. This test’s essence is to determine whether there’s a significant association between two variables, making it indispensable in research and various scientific inquiries.

Calculating the chi-square statistic can be daunting, especially when dealing with large datasets or multiple variables. This is where our Chi Square Calculator comes into play. Designed with precision and ease of use in mind, this tool demystifies the calculation process, allowing you to focus on the analysis rather than the intricacies of mathematical computations. Whether you’re a seasoned statistician or a data science enthusiast, this calculator is engineered to enhance your analytical capabilities, making sophisticated statistical analysis accessible to all.

By integrating this calculator into your workflow, you can swiftly perform chi-square tests, enabling you to draw meaningful conclusions from your data confidently. This streamlines your research process and empowers you to harness the full potential of chi-square analysis in uncovering the hidden patterns and relationships within your data.

Highlights

The Chi-Square Test demystifies relationships between categorical variables.
Our Chi Square Calculator simplifies complex statistical calculations instantly.
Real-world case studies showcase the test’s practical applications.
Step-by-step guide on leveraging the calculator for accurate results.
Understand the significance of p-value and degrees of freedom in tests.

What is the Chi-Square Test?

The Chi-Square Test is a statistical method to assess the relationship between two categorical variables. This test is pivotal in research and data analysis, mainly when examining the independence or association between variables in a dataset.

The foundation of the chi-square test lies in its ability to compare observed frequencies within a dataset to the frequencies that would be expected if there were no associations between the variables. This comparison yields the chi-square statistic, which reflects the degree of divergence between the expected and observed data.

Applications: The chi-square test is versatile, finding utility in various fields such as genetics, marketing, health sciences, and any domain where categorical data analysis is essential. It’s commonly employed to test hypotheses related to the independence of variables, for goodness-of-fit tests, and in contingency table analyses.

Significance: The value derived from the chi-square test, known as the p-value, informs researchers whether the observed associations or differences are statistically significant. A low p-value indicates that the observed data significantly deviates from what would be expected under the null hypothesis of independence, suggesting a meaningful association between the variables.

ChiSquare Calculator: Recognizing the mathematical complexity involved in chi-square calculations, especially with larger datasets or when dealing with multiple variables, the Chi-Square Calculator is designed to simplify these computations. This tool allows users to input their data and instantly receive the chi-square statistic and p-value, facilitating a more efficient and accurate analysis process. The calculator ensures that researchers can focus on interpreting the results and drawing conclusions rather than being bogged down by the computational aspects of the test.

For a more in-depth exploration of using the calculator and applying the chi-square test in real-world scenarios, continue reading as we delve into practical examples and step-by-step instructions that will enrich your understanding and application of this essential statistical tool.

Chi Square Calculator

Chi-Square Calculator

Degrees of Freedom: 1

How to Use the Chi Square Calculator

The Chi Square Calculator is a powerful tool designed to streamline the process of conducting chi-square tests, a staple in statistical analysis and research. Here’s a step-by-step guide to effectively utilize this calculator:

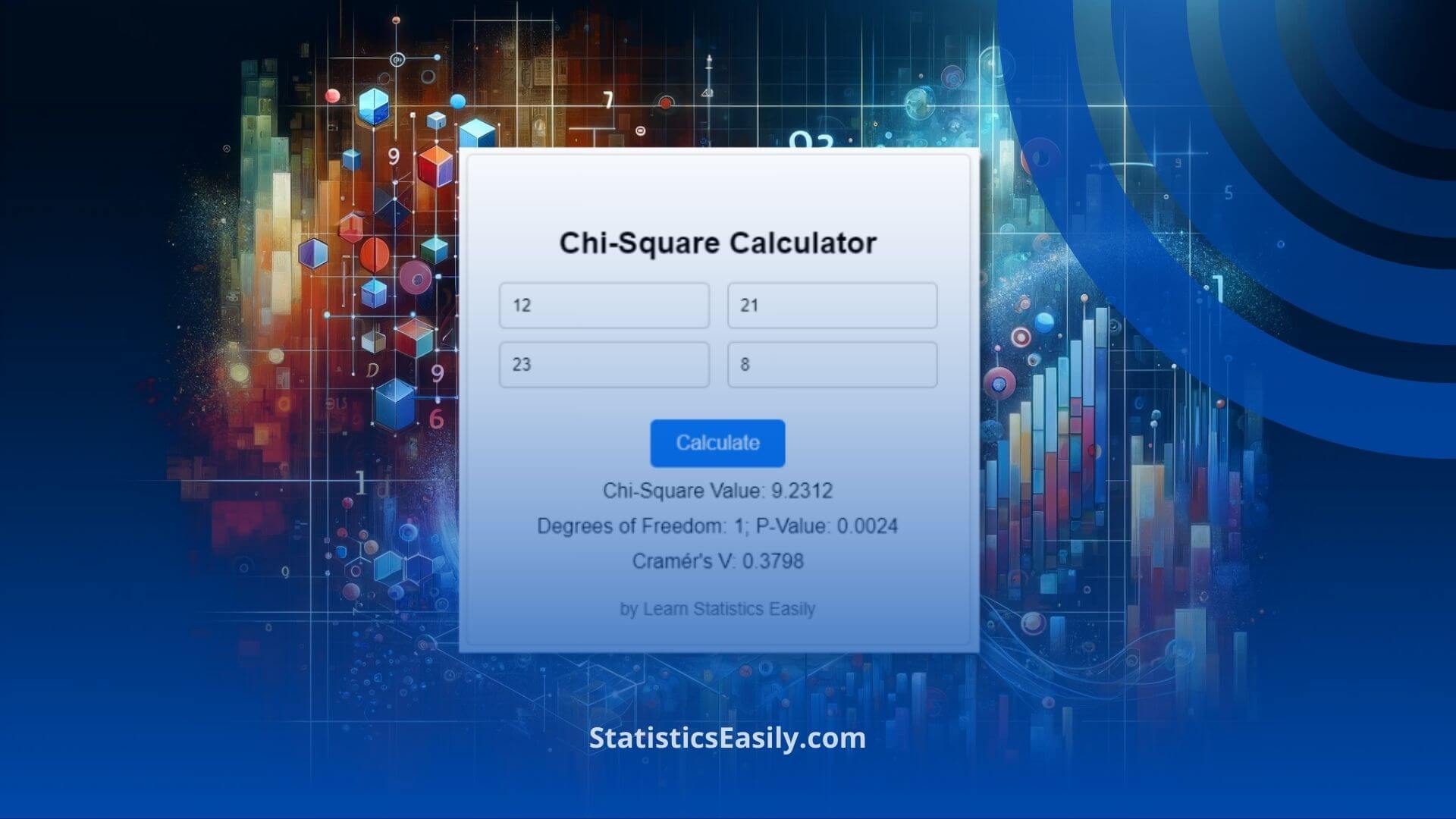
1. Input Data: Enter your observed frequencies into the designated input fields. These fields are labeled as “Value A,” “Value B,” “Value C,” and “Value D,” corresponding to the cells in a 2×2 contingency table.

2. Calculate: Once you’ve inputted your data, click the “Calculate” button.

3. Interpret Results: The results will be displayed under the calculator. You’ll see the “Chi-Square Value,” which quantifies the discrepancy between your observed and expected frequencies. A higher value indicates a greater discrepancy.

4. Degrees of Freedom: The calculator automatically considers the degrees of freedom for a 2×2 table, 1. This is crucial for determining the critical chi-square value and interpreting the p-value.

5. P-Value: The p-value is also presented, offering insight into the statistical significance of your observed associations. A p-value less than 0.05 typically suggests a significant association between the variables.

6. Effect Size: Additionally, the calculator provides Cramér’s V, a measure of effect size for chi-square tests, enabling you to gauge the strength of the association.

Cramer’s V Value	Effect Size
0.01 – 0.09	Very Small
0.10 – 0.29	Small
0.30 – 0.49	Medium
0.50 – 0.69	Large
0.70 and above	Very Large

This calculator is a computational tool and an educational resource, demystifying complex statistical concepts and making them accessible. Integrating this calculator into your analytical toolkit empowers you to conduct rigorous statistical tests confidently and precisely, unlocking deeper insights from your data.

For further exploration and to see the calculator in action with real-world data, continue to the case studies section, where we delve into practical applications of the chi-square test.

Consider visiting related articles on our blog for a more detailed guide and additional resources on chi-square tests and other statistical tools.

Case Studies or Examples

The chi-square test’s utility spans diverse fields, providing insights into the relationships between categorical variables. Below are enhanced case studies illustrating the application of chi-square tests with hypothetical data and interpretations, including effect sizes.

Marketing Research: Customer Preference Analysis

In exploring customer preferences for a new product line, a marketing team gathered data from 200 participants, divided into two age groups: under 30 and 30 or above. They wanted to see if age influenced preference for Product A vs. Product B.

Observed Frequencies:

Under 30: 70 preferred Product A, 30 preferred Product B.
30 or Above: 40 preferred Product A, 60 preferred Product B.

The chi-square test yielded a chi-square statistic of 12.59 with a p-value of 0.0004, indicating a significant association between age group and product preference. The effect size, calculated as Cramér’s V, was 0.25, suggesting a moderate relationship.

Healthcare: Treatment Efficacy Study

A study compared two treatments for a chronic condition, with 100 patients randomly assigned to Treatment X or Y. Success was defined as symptom improvement.

Observed Frequencies:

Treatment X: 45 showed improvement, 5 did not.
Treatment Y: 30 showed improvement, 20 did not.

The chi-square statistic was 8.57 with a p-value of 0.0034, signifying a significant difference in treatment efficacy. Cramér’s V was 0.29, indicating a moderate effect size.

Education: Exam Performance Analysis

An institution analyzed the impact of a preparatory course on exam success among 300 students, comparing course participants to non-participants.

Observed Frequencies:

Participants: 120 passed, 30 failed.
Non-Participants: 90 passed, 60 failed.

The chi-square test revealed a statistic of 9.22 and a p-value of 0.0024, showing a significant association between course participation and exam success. Cramér’s V of 0.17 suggested a small to moderate effect size.

Sociology: Voting Behavior Study

A study investigated voting behavior among 500 citizens across two income levels: high and low. The aim was to see if income level affected Candidate A or B’s preference.

Observed Frequencies:

High Income: 150 preferred Candidate A, 100 preferred Candidate B.
Low Income: 120 preferred Candidate A, 130 preferred Candidate B.

With a chi-square statistic of 4.76 and a p-value of 0.029, there was a significant association between income level and candidate preference. The effect size, Cramér’s V, was 0.14, indicating a small effect.

Environmental Science: Conservation Efforts Impact

This study assessed the effect of conservation efforts on an endangered species population in two areas, before and after the intervention.

Observed Frequencies:

Area 1 (Before): 80 individuals, (After): 120 individuals.
Area 2 (Before): 70 individuals, (After): 110 individuals.

The chi-square test produced a statistic of 6.67 and a p-value of 0.0098, suggesting the conservation efforts significantly impacted the species’ population. The effect size, Cramér’s V, was 0.15, showing a small to moderate relationship.

Conclusion

As we’ve explored the Chi-Square Test and its practical applications across various fields, the significance of this statistical tool in analyzing categorical data cannot be overstated. Through real-life case studies, we’ve seen how the chi-square test enables researchers and analysts to uncover significant associations between variables, providing insights that drive decision-making in marketing, healthcare, education, sociology, and environmental science.

The chi-square test’s ability to quantify the strength of association between categorical variables is invaluable, particularly when coupled with the calculation of effect sizes, such as Cramér’s V. This measure adds depth to our understanding by confirming the presence of a relationship and describing its magnitude.

For those looking to delve into statistical analysis, the chi-square test offers a gateway to more sophisticated analyses. While the calculations can be complex, especially when dealing with large datasets or multiple variables, tools like the Ch Square Calculator simplify this process, making advanced statistical analysis more accessible.

In summary, the chi-square test remains a cornerstone of categorical data analysis. Its applications extend beyond academic research, influencing marketing strategies, healthcare policy-making, educational methodologies, sociological theories, and conservation efforts in environmental science. As we continue to generate and analyze data in an increasingly digital world, the chi-square test will undoubtedly play a pivotal role in transforming raw data into actionable insights.

We encourage readers to integrate the chi-square test into their analytical repertoire, leveraging tools like the Chi Square Calculator to enhance their research and data analysis capabilities. For those keen to explore further, consider diving into the wealth of resources available on statistical analysis, where the journey from data to discovery is just a calculation away.

Frequently Asked Questions (FAQs)

Q1: What is a Chi-Square Test? A Chi-Square Test is a statistical method used to analyze the relationship between two categorical variables, determining whether they have a significant association or independence. It’s essential in marketing, healthcare, education, and more.

Q2: How is the Chi-Square statistic calculated? The Chi-Square statistic is calculated by summing the squared difference between observed and expected frequencies, divided by the expected frequencies for each category. This quantifies the discrepancy between what is observed in the data and what would be expected if there was no association.

Q3: What does the p-value in a Chi-Square Test indicate? The p-value helps determine the significance of the results. For instance, a p-value less than 0.05 suggests that the observed association is statistically significant and not due to random chance.

Q4: Can the Chi-Square Test be used for large datasets? Yes, the Chi-Square Test can be applied to large datasets. However, it’s crucial to ensure that the expected frequencies in each contingency table cell are sufficient (usually at least 5) to maintain the validity of the test.

Q5: What are the degrees of freedom in a Chi-Square Test? Degrees of freedom in a Chi-Square Test typically equal the number of categories in each variable minus one, multiplied together. For a 2×2 table, this would be (2-1)*(2-1) = 1.

Q6: How does sample size affect a Chi-Square Test? The sample size can significantly impact the test’s sensitivity. Larger samples can detect smaller differences as significant, whereas smaller samples might not detect the same effect.

Q7: Is the Chi-Square Test applicable only to 2×2 contingency tables? While commonly used for 2×2 tables, the Chi-Square Test can be applied to larger contingency tables, analyzing the association between variables with more than two categories.

Q8: How do you interpret Cramér’s V? Cramér’s V is an effect size measure for Chi-Square Tests, indicating the strength of association between the variables. Values range from 0 (no association) to 1 (perfect association), with small, medium, and large effects thresholds.

Q9: What is the difference between the Chi-Square Test of Independence and the Chi-Square Goodness-of-Fit Test? The Test of Independence assesses the relationship between two categorical variables. At the same time, the Goodness-of-Fit Test compares observed frequencies to expected frequencies for a single categorical variable across different categories.

Q10: How can a Chi-Square Test impact decision-making? The Chi-Square Test can guide strategic decisions in marketing campaigns, healthcare policies, educational programs, and more by revealing significant associations between variables and ensuring data-informed actions.

Chi-Square Calculator: Enhance Your Data Analysis Skills

Introduction

Highlights

What is the Chi-Square Test?

Chi Square Calculator

Chi-Square Calculator

How to Use the Chi Square Calculator