Absolute Mean Deviation: Demystifying the Key Statistics Concept
In data analysis, understanding certain key concepts can illuminate the meaning behind the numbers. One such concept is the Absolute Mean Deviation (AMD). This statistical measure provides valuable insight into the dispersion of a dataset. So let’s take a look into the AMD.
What is Absolute Mean Deviation?
The Absolute Mean Deviation is a measure that tells us how the numbers in a data set are spread out. Specifically, it represents the average distance between each data point and the dataset mean. Calculating the AMD involves three primary steps:
1. Determining the mean of the dataset
2. Finding the absolute deviation of each data point from the mean
3. Calculating the mean of these absolute deviations
It is worth noting that AMD differs from the mean deviation, which does not take the absolute values of the deviations. As a result, the mean deviation can mislead us about the dataset’s variability due to positive and negative deviations canceling each other out. In contrast, by considering absolute deviations, the AMD ensures that all deviations contribute to the overall measure of dispersion, making it a more reliable indicator of variability.
Highlights
- Absolute mean deviation represents the average distance between each data point and the dataset’s mean.
- Standard deviation and absolute mean deviation both quantify data dispersion, but standard deviation’s squaring places more weight on larger deviations.
- Absolute mean deviation is more efficient, easier to use, and more understandable than the standard deviation.
- Finding absolute mean deviation involves calculating the dataset’s mean, finding absolute deviations, and then finding these absolute deviations’ mean.
- Absolute mean deviation is resilient to outliers, errors, and non-normal distributed data, making it useful in real-world situations.
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Absolute Mean Deviation vs. Standard Deviation
Standard deviation (SD) is another common measure of dispersion. It shares some similarities with the absolute mean deviation, such as quantifying the dispersion of data points around the mean. However, there are some key differences. The standard deviation squares the deviations from the mean, while the AMD takes absolute values. This squaring in standard deviation places more weight on larger deviations, which may skew the measure of dispersion if the dataset contains outliers.
In a article published in the British Journal of Educational Studies, Gorard (2005) argues for the advantages of AMD over standard deviation. He notes that AMD is more efficient in estimating a population parameter, particularly in real-life situations where data contain tiny errors or do not form a normal distribution. Moreover, AMD is easier to use and understand, making it an accessible tool for new researchers.
A Five-step Approach to Finding the Absolute Mean Deviation
Finding the absolute mean deviation of a dataset is straightforward and can be conducted in five steps:
1. Calculate the mean (average) of the dataset.
2. To obtain the deviations, subtract the mean from each data point.
3. Take the absolute value of each deviation.
4. Sum up these absolute deviations.
5. Divide the sum by the data points number in the dataset.
| Step | Description | Calculation | Result |
|---|---|---|---|
| 1 | Calculate the mean | (2 + 4 + 6 + 8 + 10) / 5 | 6 |
| 2 | Subtract the mean from each data point and take the absolute value | |2-6|, |4-6|, |6-6|, |8-6|, |10-6| | 4, 2, 0, 2, 4 |
| 3 | Calculate the average of these absolute deviations (Absolute Mean Deviation) | (4 + 2 + 0 + 2 + 4) / 5 | 2.4 |
This process ensures that each data point contributes to the overall measure of dispersion, capturing a more comprehensive picture of the dataset’s variability.
Calculating Absolute Mean Deviation in Excel
Excel offers a convenient platform for calculating absolute mean deviation. Here are the steps:
1. Enter your data into a single column.
2. Use the AVERAGE function to calculate the mean of the data.
3. Subtract the mean from each data point in a new column to find the deviations.
4. Use the ABS function to take the absolute value of each deviation.
5. Use the SUM function to add up all the absolute deviations.
6. Finally, divide this sum by the number of data points to get the AMD.
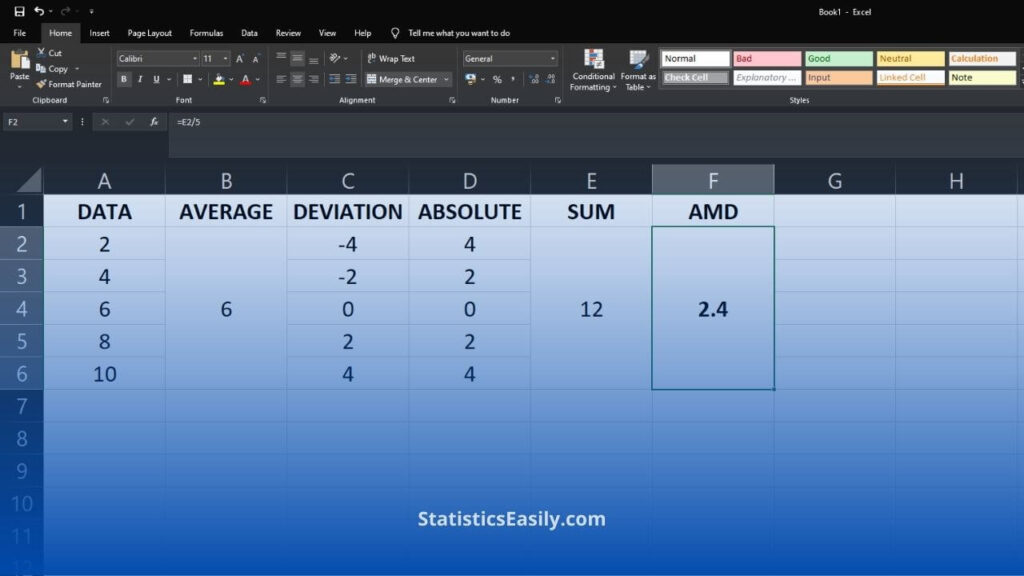
While Excel doesn’t have a built-in function for AMD, this process is straightforward and allows for efficient computation of AMD.
Why is Absolute Mean Deviation Important?
Understanding the Absolute Mean Deviation is crucial because it provides a clear, accessible, and reliable measure of dispersion. AMD effectively highlights the variability in a dataset, helping analysts and researchers interpret their data more accurately. Furthermore, it’s resilient to outliers and errors, making it a valuable tool in real-world situations where data rarely adhere perfectly to statistical assumptions.
While standard deviation remains a widely used measure of dispersion, awareness and understanding of AMD can offer a broader toolkit for analyzing and interpreting data. This, in turn, contributes to more robust and nuanced insights, whether you’re conducting academic research or making data-driven decisions in business, public policy, or other fields.
In conclusion, while the AMD might not be as well-known as the standard deviation, its utility and robustness make it invaluable in statistics and data analysis. So, if you’re dealing with data, it’s worth getting acquainted with the Absolute Mean Deviation.
Reference: Gorard, S. (2005), REVISITING A 90-YEAR-OLD DEBATE: THE ADVANTAGES OF THE MEAN DEVIATION. British Journal of Educational Studies, 53: 417-430. https://doi.org/10.1111/j.1467-8527.2005.00304.x
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Recommended Articles
Interested in deepening your understanding of essential statistics concepts? Take advantage of other insightful articles on our blog.
- Standard Deviation Calculator
- What Is The Standard Deviation?
- Standard Deviation Rules Misconceptions
- Can Standard Deviations Be Negative?
- Exploring Standard Deviation
- How Standard Deviation is Calculated
- Can Standard Deviations Be Negative? (Story)
- Random Sampling on Excel: An In-depth Analysis
Frequently Asked Questions (FAQs)
It’s a statistical measure that represents the average distance between each data point and the dataset mean.
Absolute mean deviation considers absolute deviations, ensuring all deviations contribute to the overall measure of dispersion, unlike mean deviation.
While both measure dispersion, standard deviation squares the deviations, potentially skewing the dispersion measure if the dataset contains outliers.
Absolute mean deviation is more efficient, easier to use, and understand than standard deviation, particularly in real-world data situations.
Calculate the dataset’s mean, find each data point’s absolute deviation from the mean, and then find these absolute deviations’ mean.
Use a series of steps involving AVERAGE, ABS, and SUM functions to calculate AMD in Excel.
Absolute mean deviation considers absolute deviations, ensuring all deviations, including outliers, contribute to the overall dispersion measure.
Absolute mean deviation reveals the degree of variability in a dataset, providing a clear and reliable measure of dispersion to aid accurate data interpretation.
Absolute mean deviation provides a reliable measure of dispersion, complementing other tools like standard deviation for a more nuanced data interpretation.
Absolute mean deviation provides a robust measure of data dispersion, aiding in the accurate interpretation of data for academic research or data-driven decisions.








