Parametric vs. Nonparametric Tests: Choosing the Right Tool for Your Data
You will learn the distinctions between Parametric vs. Nonparametric Tests and their applications in data analysis.
Introduction
Have you ever stood before a dataset and wondered which statistical test it should use? Choosing between Parametric vs. Nonparametric Tests is a technical decision about aligning your analysis with the nature of your data to ensure truthful, reliable insights. This article aims to demystify these two paths in statistical testing, guiding you toward making an informed choice based on the essence of your data. Through an explicit exploration of Parametric vs. Nonparametric Tests, we’ll equip you with the knowledge to choose the right tool for your data, ensuring your analysis is robust and reflects the data’s inherent truth.
Highlights
- Understanding assumptions behind parametric tests reveals their ideal conditions for usage.
- Nonparametric tests offer robustness without strict distribution requirements and are suitable for diverse datasets.
- A comparison chart demystifies when to use parametric versus nonparametric tests, aligning with data integrity.
- Real-world case studies illustrate the impactful choice between parametric and nonparametric tests in analysis.
- Advancements in statistical testing enhance our ability to uncover deeper truths within complex datasets.
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Understanding Parametric Tests
Parametric tests serve as a fundamental tool in statistical analysis. They are predicated on the assumption that the data follows a specific distribution, usually normal. These tests require that the data adhere to certain criteria, including interval or ratio level measurements, a defined distribution, and homogeneity of variance among groups.
Among the most utilized parametric tests are the t-test and ANOVA. The t-test is designed to compare the means of two groups, helping to determine if there are significant differences between them. On the other hand, ANOVA (Analysis of Variance) allows for the comparison of means across three or more groups, offering a broader application for statistical analysis.
The core of parametric testing lies in its logic and methodology, allowing for more powerful and precise conclusions when its assumptions are met. This precision stems from the tests’ ability to effectively utilize sample data, making them invaluable in scenarios where the underlying assumptions about the data distribution are satisfied. By applying these tests, researchers and analysts can extract meaningful insights from their data, guided by a framework emphasizing accuracy and reliability.
Exploring Nonparametric Tests
Nonparametric tests are a crucial component in the statistical analysis toolkit, especially when data does not meet the stringent assumptions required for parametric tests. These tests are used when data distribution is unknown or when dealing with ordinal or nominal data that do not satisfy the normal distribution criteria.
Critical nonparametric tests include the Mann-Whitney U test and the Kruskal-Wallis test. The Mann-Whitney U test compares differences between two independent samples, offering an alternative to the t-test when data do not follow a normal distribution. The Kruskal-Wallis test, on the other hand, is a method for comparing more than two groups. It serves as the nonparametric counterpart to ANOVA, allowing for analysis without normality.
The flexibility and robustness of nonparametric testing make it invaluable across various data scenarios. These tests do not assume a specific distribution, making them adaptable to a broader range of data types and distributions. This versatility ensures that statistical analysis is accessible even when data are not perfectly aligned with the ideal conditions for parametric testing, thus maintaining the integrity and reliability of the analysis. Through nonparametric methods, researchers can confidently analyze data that would otherwise be challenging to interpret, ensuring no valuable insight is overlooked due to the limitations of the data’s distribution.
| Parametric Test | Nonparametric Test |
|---|---|
| Independent samples t-test | Mann-Whitney U Test |
| Paired samples t-test | Wilcoxon Signed-rank Test |
| One-way ANOVA | Kruskal-Wallis H Test |
| One-way repeated measures ANOVA | Friedman Test |
Comparing Parametric vs. Nonparametric Tests
When selecting a statistical test, the decision must reflect the data’s structure and the research question’s precision. The comparison of Parametric vs. Nonparametric Tests often centers on their assumptions and applicability to various data types.
Parametric tests are often more potent and have a higher sensitivity in detecting true effects when their strict assumptions are met. They are ideal when data distributions are known and meet the assumptions of normality, homoscedasticity, and interval or ratio scale. In contrast, nonparametric tests do not assume a specific data distribution. They are, therefore, more flexible suitable for ordinal data, or when the sample size is too small to validate the distribution assumptions. They are handy for skewed data distributions or when dealing with outliers.
The choice between these tests is also critical in ethical terms. Accurate data representation is paramount in scientific inquiry, with integrity and without distortion. Therefore, applying the correct statistical test is not only a methodological choice but an ethical one, ensuring that the conclusions drawn are a truthful reflection of the underlying phenomena.
Scenarios where nonparametric tests might be preferred include small sample sizes, which make it challenging to ensure that parametric assumptions are met. They are also chosen when data are measured on an ordinal scale, which does not fit parametric test interval or ratio scale requirements.
Conversely, parametric tests are often employed when dealing with large samples where the central limit theorem assures normality in the means distribution or when prior analysis demonstrates that the data follow a specific distribution.
In summary, the decision to use parametric or nonparametric tests hinges on statistical considerations and the ethical presentation of data. One must weigh the assumptions and conditions of the dataset against the potential impact and interpretation of the results, always striving for the most honest and accurate reflection of reality.
| Parametric Tests | Nonparametric Tests |
|---|---|
| Assume a specific distribution (often normal) | Do not assume a specific distribution |
| More powerful when assumptions are met | Less powerful but more flexible |
| Typically used for larger sample sizes | Can be used for smaller sample sizes |
| Sensitive to outliers | More robust to outliers |
| Data must be at least interval or ratio scale | Suitable for ordinal or nominal data |
Practical Guide to Choosing Between Parametric vs. Nonparametric Tests
Selecting the appropriate statistical test is a decision of utmost significance, impacting the validity of your research conclusions. A structured approach to this decision involves a series of questions that guide the researcher to the most suitable test based on the data’s characteristics.
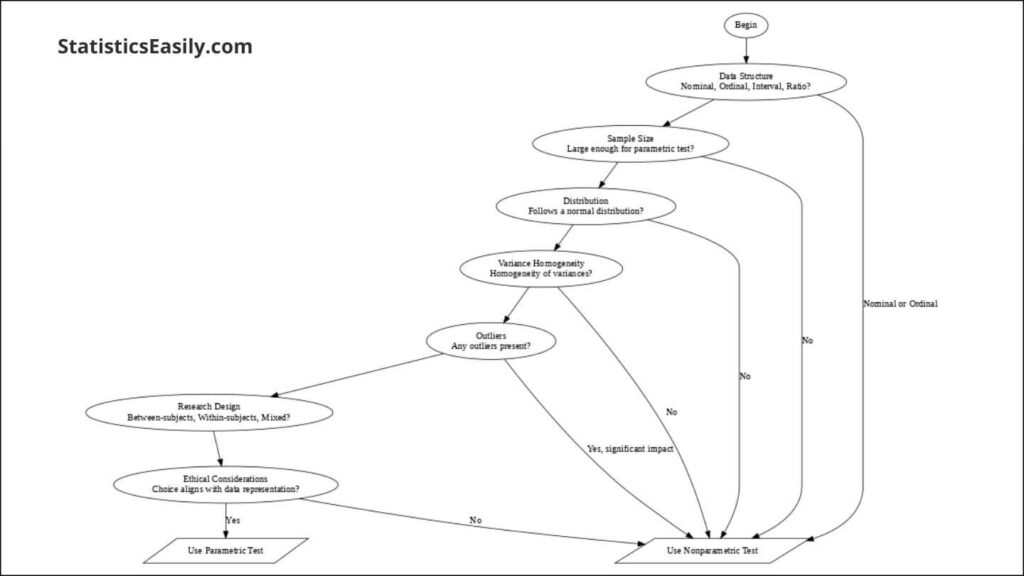
Decision Tree for Choosing the Right Test:
- Data Structure: Begin by examining the scale of measurement. Is your data nominal, ordinal, interval, or ratio?
- Sample Size: Is your sample size large enough to satisfy the assumptions of a parametric test?
- Distribution: Does your sample data follow a normal distribution? Utilize graphical analysis or statistical tests of normality to decide.
- Variance Homogeneity: Do your data demonstrate homogeneity of variances for comparing groups? Levene’s test can help assess this.
- Outliers: Are there outliers present, and how might they impact your analysis?
- Research Design: Is the study design between-subjects, within-subjects, or mixed?
- Ethical Considerations: Ensure that the choice of test aligns with a genuine and ethical representation of the data.
Case Study Example:
Imagine you are researching the effect of a new educational technique on students’ test scores. You have scores from before and after applying the method to a relatively small class of students.
- Data Structure: The test scores are ratio data.
- Sample Size: With a small class, the sample size may be inadequate for parametric tests.
- Distribution: Preliminary analysis reveals the data are not normally distributed.
- Variance Homogeneity: This cannot be reliably assessed, given the small sample size.
- Outliers: There are no significant outliers.
- Research Design: The design is within-subjects, as the same students are measured before and after the intervention.
- Ethical Considerations: A nonparametric test would represent the impact truthfully, considering data with a non-normal distribution and a small sample size.
In this scenario, a nonparametric test such as the Wilcoxon signed-rank test would be appropriate to compare the before and after scores.
This guide emphasizes the importance of choosing a test that represents the data’s truth as the cornerstone of research integrity. Each decision point in the tree is an opportunity to affirm that the statistical method selected aligns with scientific and ethical standards, ensuring that the findings you report are a reliable and accurate reflection of the data’s story.
Ad Title
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusion
In navigating the terrain of statistical analysis, distinguishing Parametric vs. Nonparametric Tests is crucial. We’ve traversed the underlying assumptions that guide the choice of parametric tests and their reliance on data adhering to a specific distribution, primarily normal. With their adaptability, nonparametric tests have been underscored as valuable when data do not meet these stringent assumptions, providing a robust alternative. The comparison of these tests underscores the importance of selecting the method that aligns with the dataset’s nature and the study’s design, underpinning the results’ validity and reliability.
This article has illuminated that ethical considerations are paramount beyond methodology. It advocates for a choice of statistical test that offers a truthful representation of data, thus ensuring the integrity of research findings. As we close, let’s reiterate the invitation to approach data analysis with the due diligence it demands, always marrying technical precision with ethical responsibility and upholding the pillars of truth in our quest for knowledge.
Recommended Articles
Explore our collection of articles on related statistical topics to discover more insights and elevate your data analysis skills. Dive deeper into the world of statistics with us today.
- Mastering One-Way ANOVA: A Comprehensive Guide for Beginners
- Common Mistakes to Avoid in One-Way ANOVA Analysis
- A Comprehensive Guide to Hypotheses Tests in Statistics
- Nonparametric Statistics – an overview (External Link)
- Non-Parametric Statistics: A Comprehensive Guide
- A Guide to Hypotheses Tests (Story)
Frequently Asked Questions (FAQs)
Q1: What are Parametric Tests? They’re statistical tests that assume data follows a specific distribution. They’re typically used for hypothesis testing with quantitative data.
Q2: What situations call for Nonparametric Tests? When data doesn’t meet the assumptions necessary for parametric tests, such as unknown distributions or ordinal data.
Q3: Can you give examples of Parametric Tests? Examples include the t-test for comparing means and ANOVA for comparing means across multiple groups.
Q4: Are Nonparametric Tests less powerful than parametric ones? Not necessarily. While parametric tests are more potent with assumptions met, nonparametric tests are more flexible and robust under assumption violations.
Q5: How do I decide between a Parametric and Nonparametric Test? Decision-making involves evaluating data distribution, scale of measurement, and sample size, among other factors.
Q6: What is a common Nonparametric Test for two independent samples? The Mann-Whitney U test is commonly used to compare two independent samples when parametric assumptions aren’t met.
Q7: Can Parametric Tests be used on ranked data? Typically, no. Ranked data violates the assumption of interval or ratio scale required for most parametric tests.
Q8: How do technological advancements affect the choice between Parametric and Nonparametric Tests? Technological advancements enable more complex data analysis, potentially influencing the preference for nonparametric methods when dealing with intricate data patterns.
Q9: Why is understanding the assumptions behind tests critical in statistical analysis? It ensures the integrity and validity of the analysis results, aligning with the ethical considerations in representing data truthfully.
Q10: What role do Parametric and Nonparametric Tests play in data-driven decision-making? They are essential tools for hypothesis testing, enabling informed decisions based on statistical evidence and rigorous analysis.








